2진법 과 16진법 완벽 기초 이해, 2진법 16진법 변환 방법, 16진법을 사용하는 이유.

진법이란?

컴퓨터를 배우다 보면 "진법"이라는 용어를 자주 접하게 됩니다. 진법은 숫자를 표현하는 방법인데요. 우리가 일상에서 사용하는 숫자 체계는 10진법이라고 합니다. 0부터 9까지의 숫자를 사용하죠. 하지만 컴퓨터는 2진법과 16진법을 주로 사용합니다. 오늘은 왜 그런지, 어떻게 사용하는지 알아보고, 2진법을 16진법으로 변환하는 방법도 설명해드리겠습니다. 

 2진법 (Binary)

2진법이란?

2진법은 오직 두 개의 숫자, 0과 1만을 사용하는 숫자 체계입니다. 컴퓨터는 전기 신호(전기가 있거나 없거나)를 기반으로 작동하기 때문에 2진법이 아주 적합합니다.

2진법 숫자 읽기

2진법은 오른쪽에서 왼쪽으로 각 자리마다 2의 제곱 값을 가지게 됩니다. 예시를 보면서 연습을 해보면 좀 더 빠르게 이해할 수 있는데요. 

예를 들어, 1010이라는 2진수를 보면:

• 오른쪽에서 첫 번째 자리: $0\times 2⁰{\mathrm{ }}^{}= 0$
• 두 번째 자리: $1\times {\mathrm{2¹}}^{\mathrm{ }}= 2$
• 세 번째 자리: $0\times 2²{\mathrm{ }}^{}= 0$
• 네 번째 자리: $1\times 2³{\mathrm{ }}^{}= 8$

이를 모두 더하면 8 + 2 = 10이 됩니다. 즉, 2진법 1010은 10진법으로 10을 의미합니다.

2진법으로 숫자 변환하기

10진법 숫자 13을 2진법으로 변환해볼게요.

1. 13을 2로 나눕니다. 몫은 6, 나머지는 1
2. 6을 2로 나눕니다. 몫은 3, 나머지는 0
3. 3을 2로 나눕니다. 몫은 1, 나머지는 1
4. 1을 2로 나눕니다. 몫은 0, 나머지는 1입니다.

나머지를 역순으로 읽으면 1101이 됩니다. 즉, 13은 2진법으로 1101 이 되죠. 

16진법 (Hexadecimal)

16진법이란?

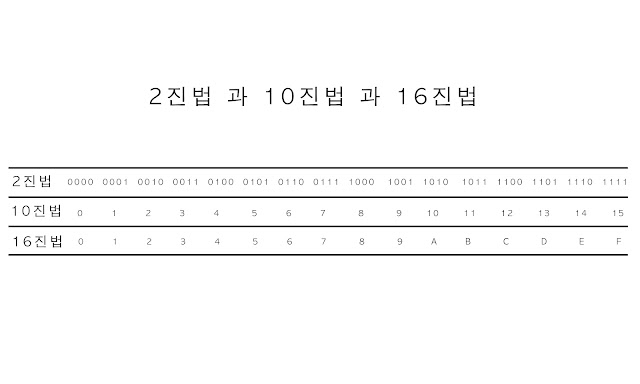
16진법은 0부터 9까지의 숫자와 A부터 F까지의 알파벳을 사용합니다. A는 10, B는 11, C는 12, D는 13, E는 14, F는 15를 의미합니다.

16진법 숫자 읽기

16진법도 각 자리마다 16의 제곱 값을 가지게 되는데요. 

예를 들어, 1A3이라는 16진수를 보면:

• 오른쪽에서 첫 번째 자리: $3\times 1{\mathrm{6⁰}}^{}=3$
• 두 번째 자리: $A\times 1{\mathrm{6¹ }}^{}= 10\times \mathrm{16 }= 160$
• 세 번째 자리: $1\times 1{\mathrm{6² }}^{}= 1\times \mathrm{256 }= 256$

이를 모두 더하면 256 + 160 + 3 = 419가 됩니다. 즉, 16진법 1A3은 10진법으로 419를 의미하죠. 

16진법으로 숫자 변환하기

10진법 숫자 254를 16진법으로 변환해보겠습니다.

1. 254를 16으로 나눕니다. 몫은 15, 나머지는 14
   • 14는 16진법으로 E입니다.
2. 15를 16으로 나눕니다. 몫은 0, 나머지는 15
   • 15는 16진법으로 F입니다.

나머지를 역순으로 읽으면 FE가 되죠. 즉, 254는 16진법으로 FE입니다.

이때 유의해서 기억해야 할 점이 있다면,  10진법을 2진법으로 변환 할때와 10진법을 16진법으로 번환할 때, 나머지 수를 배열하는 순서가 다르다는 점입니다.  

2진법과 16진법 변환

2진법 숫자를 16진법으로 변환하는 방법은 2진법 숫자를 네 자리씩 묶어서 16진법으로 바꾸면 되는데요. 처음에는 조금 헷갈릴 수 있지만, 연습을 몇번만 해보시면, 금방 이해하실 수 있어요. 

예를 들어, 2진법 11010111을 16진법으로 변환해볼게요

• 네 자리씩 묶으면 1101 0111 이죠.
• 각 묶음을 16진법으로 바꿔 줄게요. 
  • 1101은 16진법으로 D
  • 0111은 16진법으로 7입니다.

그래서 11010111은 16진법으로 D7 이 됩니다. 

컴퓨터에서 16진법을 사용하는 이유. 

컴퓨터를 배우다 보면 "16진법"이라는 용어를 자주 접하게 됩니다. 저는 16진법에 대해 공부하면서  우리에게 익숙한 10진법 대신 왜 16진법을 사용하는지 궁금했는데요. 간단하게 16진법이 컴퓨터에서 중요한 이유를 쉽게 설명해드리겠습니다.

1. 컴퓨터의 기본 단위와의 호환성

컴퓨터는 2진법, 즉 0과 1로 데이터를 처리합니다. 하지만 2진법은 숫자가 길어질 수 있죠. 예를 들어, 10진법 숫자 255는 2진법으로 11111111입니다. 이렇게 긴 숫자열을 읽고 쓰는 것은 실수할 가능성이 높고 비효율적입니다. 

2진법과 16진법의 비교

16진법은 0부터 9까지의 숫자와 A부터 F까지의 알파벳을 사용합니다. 이렇게 하면 2진법 숫자 4자리를 한 자리로 표현할 수 있습니다. 예를 들어, 2진법 1111은 16진법으로 F가 됩니다. 이렇게 표현하면 훨씬 간결해집니다.

2. 변환의 용이성

2진법 숫자를 16진법으로 변환하는 과정은 간단합니다. 2진법 숫자를 네 자리씩 묶어서 16진법으로 바꾸기만 하면 되죠. 예를 들어, 2진법 110110111101을 16진법으로 변환한다면,

• 2진법: 1101 1011 1101 (네 자리씩 묶음)
• 16진법: D B D

이런 변환 과정을 통해 2진법을 더 짧고 쉽게 이해할 수 있는 16진법으로 표현할 수 있습니다.

3. 큰 숫자의 간결한 표현

2진법을 직접 사용하면 숫자가 매우 길어지지만, 16진법을 사용하면 그 길이를 크게 줄일 수 있습니다. 예를 들어, 10진법 숫자 65535는 2진법으로 1111111111111111이지만, 16진법으로는 FFFF입니다. 이처럼 큰 숫자를 간결하게 표현할 수 있습니다. 정말 큰 차이죠 ? 

4. 메모리 주소 및 디버깅에서의 편리함

프로그래밍과 컴퓨터 시스템에서 메모리 주소는 매우 중요한 역할을 합니다. 메모리 주소는 일반적으로 매우 큰 숫자로 이루어져 있습니다. 16진법으로 표현하면 더 간결하고 관리하기 쉬워집니다. 예를 들어, 10진법 메모리 주소 1048576은 16진법으로 100000입니다.

디버깅 과정에서도 16진법은 중요한 역할을 합니다. 많은 디버거 도구는 메모리 내용을 16진법으로 표시하여 프로그래머가 더 쉽게 데이터를 분석하고 오류를 찾을 수 있도록 합니다.

결론

2진법과 16진법은 컴퓨터에서 아주 중요한 숫자 체계입니다. 2진법은 컴퓨터가 데이터를 처리하는 기본 방식이고, 16진법은 사람이 데이터를 읽기 쉽게 만들어줍니다.

16진법의 장점 요약

• 컴퓨터의 기본 단위와의 호환성: 2진법 숫자를 더 간결하게 표현할 수 있습니다.
• 변환의 용이성: 2진법 숫자를 쉽게 16진법으로 변환할 수 있습니다.
• 큰 숫자의 간결한 표현: 긴 2진법 숫자를 짧게 표현할 수 있습니다.
• 메모리 주소 및 디버깅에서의 편리함: 메모리 주소와 디버깅 과정에서 효율적입니다.

이러한 이유로 컴퓨터 관련 작업에서 16진법이 사람이 읽기 쉽고, 더 효율적인 숫자 체계로 사용됩니다.